Battling Mechanics
A brief overview of battling mechanics, meta, factions and full sets
Last updated
Was this helpful?
A brief overview of battling mechanics, meta, factions and full sets
Last updated
Was this helpful?
The Core Battling Mechanics of Banana.Capital center on two primary elements: Items Damage and Damage Factions. Each banana set is comprised of 4 main set pieces:
Head piece
Body Armor
Weapon
Banana peel🍌 skin
Each of these NFT items belongs to a specific faction and possesses its unique damage value. The default mechanism involves calculating the damage based on its intrinsic damage value and the faction modifiers when pitted against opposing set factions.
For example, let's consider a Red headpiece with a damage value of 5.00.
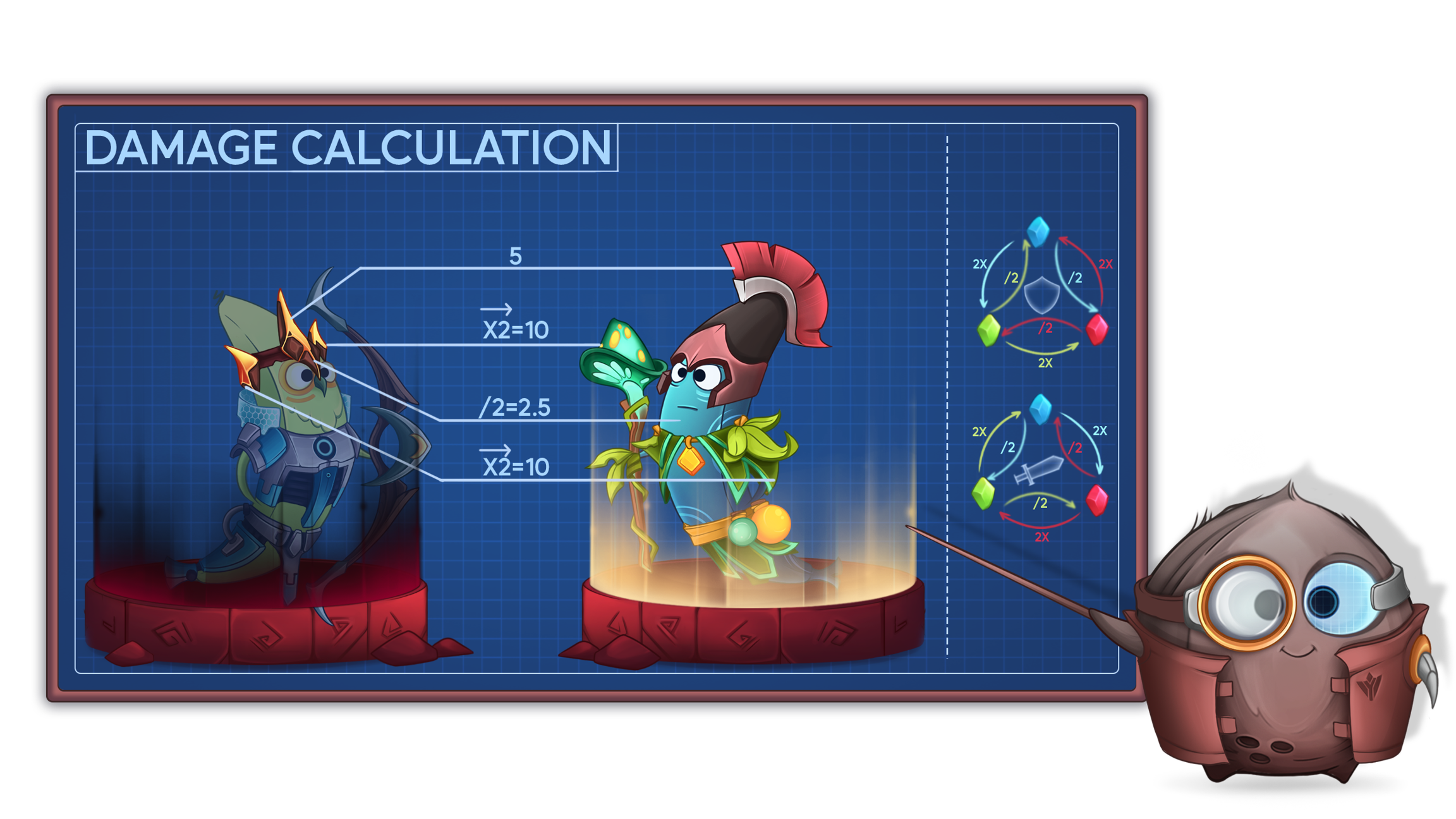
To calculate the cumulative damage against a set with a Red headpiece, Blue skin, Green body armor, and Green weapon, we use the following formula:
(5.00 vs Red headpiece) + (2.50 vs Blue skin, since Red deals reduced damage to Blue) + (10.00 vs Green body armor, since Red deals increased damage to Green) + (10.00 vs Green weapon) = 27.50 for a Red headpiece with a damage value of 5.00.
The defense of the item is calculated in a similar fashion but is contingent on an inverse faction rotation.
❖ Red headpiece (damage 3.50)
❖ Red headpiece (damage 7.00)
❖ Green skin (damage 2.00)
❖ Green skin (damage 2.50)
❖ Blue body armor (damage 5.50)
❖ Blue body armor (damage 8.00)
❖ Green weapon (damage 6.00)
❖ Red weapon (damage 4.00)
Calculating combined damage for both sets:
❖ Red headpiece: (3.50 vs Red headpiece) + (7.00 vs Green skin) + (1.75 vs Blue body armor) + (3.50 vs Red weapon) = 15.75
❖ Red headpiece: (7.00 vs Red headpiece) + (14.00 vs Green skin) + (3.50 vs Blue body armor) + (14.00 vs Green weapon) = 38.50
❖ Green skin: (1.00 vs Red headpiece) + (2.00 vs Green skin) + (4.00 vs Blue body armor) + (1.00 vs Red weapon) = 8.00
❖ Green skin: (1.25 vs Red headpiece) + (2.50 vs Green skin) + (5.00 vs Blue body armor) + (2.50 vs Green weapon) = 11.25
❖ Blue body armor: (11.00 vs Red headpiece) + (2.75 vs Green skin) + (5.50 vs Blue body armor) + (11.00 vs Red weapon) = 30.25
❖ Blue body armor: (16.00 vs Red headpiece) + (4.00 vs Green skin) + (8.00 vs Blue body armor) + (4.00 vs Green weapon) = 32.00
❖ Green weapon: (3.00 vs Red headpiece) + (6.00 vs Green skin) + (12.00 vs Blue body armor) + (3.00 vs Red weapon) = 24.00
❖ Red weapon: (4.00 vs Red headpiece) + (8.00 vs Green skin) + (2.00 vs Blue body armor) + (8.00 vs Green weapon) = 22.00
Summed up:
Total Damage: 78.00
Total Damage: 103.75
Total Defense: 81.75
Total Defense: 99.25
The final comparison and the duel outcome is then decided based on formula:
(Set A Defense - Set B Damage) Vs (Set B Defense - Set A Damage)
❖ Red headpiece (damage 6.00)
❖ Red headpiece (damage 7.00)
❖ Red skin (damage 5.00)
❖ Green skin (damage 5.00)
❖ Red body armor (damage 7.00)
❖ Blue body armor (damage 9.00)
❖ Red weapon (damage 9.00)
❖ Red weapon (damage 10.00)
Calculating combined damage for both sets:
❖ Red headpiece: (6.00 vs Red headpiece) + (12.00 vs Green skin) + (3.00 vs Blue body armor) + (6.00 vs Red weapon) = 27.00
❖ Red headpiece: (7.00 vs Red headpiece) + (7.00 vs Red skin) + (7.00 vs Red body armor) + (7.00 vs Red weapon) = 28.00
❖ Red skin: (5.00 vs Red headpiece) + (10.00 vs Green skin) + (2.50 vs Blue body armor) + (5.00 vs Red weapon) = 22.50
❖ Green skin: (2.50 vs Red headpiece) + (2.50 vs Red skin) + (2.50 vs Red body armor) + (2.50 vs Red weapon) = 10.00
❖ Red body armor: (7.00 vs Red headpiece) + (14.00 vs Green skin) + (3.50 vs Blue body armor) + (7.00 vs Red weapon) = 31.50
❖ Blue body armor: (18.00 vs Red headpiece) + (18.00 vs Red skin) + (18.00 vs Red body armor) + (18.00 vs Red weapon) = 72.00
❖ Red weapon: (9.00 vs Red headpiece) + (18.00 vs Green skin) + (4.50 vs Blue body armor) + (9.00 vs Red weapon) = 40.50
❖ Red weapon: (10.00 vs Red headpiece) + (10.00 vs Red skin) + (10.00 vs Red body armor) + (10.00 vs Red weapon) = 40.00
Calculating combined damage for both sets:
But if we just replace the set A with a full set combo and therefore gain a 50% damage reduction all of a sudden the outcome is opposite:
We introduced Full Set bonuses to give a fair chance to a singular faction sets as they tended to under-perform compared to mixed sets mainly because of their inability to counter chunk of countering faction damage.
This mechanic was introduced to promote a healthy balance between "mixing & matching" behaviours and as a result encourage trading of specific set items between players.
Note: exact bonus percentages and full set mechanic specifics may be changed over time based on meta and battle statistics. The desired outcome is for 1 faction sets to have roughly equal to mixed set win rates with a 5-10% deviation tolerance.
